Week 6: graphs

Subsite home page:  http://bit.ly/focs-aux

General strategy

(This is not really code, nor pseudocode.)

This is a description of what the algorithm does. This description is closer than the textual algorithm given in the lecture at 08:00 .

Initialise the search tree using the initial state of the problem.

Loop:

1. If there are no candidates for expansion, then return failure.
2. Choose a leaf node.
3. If the chosen leaf matches the goal, then return the leaf.
4. If not, then expand the node, and use the strategy to determine how to re-order the new list of candidates, and perhaps filter out the visited nodes.

Note: depending on the expansion, goal, and strategy, there are two reasons why this might never finish.

(answer goes here)

1. If we don’t filter out visited nodes, it’s easy to get in an infinite loop.
2. If we filter out visited nodes, but there are infinitely many possible nodes, then we can get in an infinite loop.

Exercise: why did we not get in an infinite loop when we searched for the path from B to A in the lecture?

Version 1

(* basic algo *)

(* Note that this version does *not* use 'visited'. So
   the type of 'strategy' is different.

 *)

let rec search
    (graph : (char * char * int) list)
    expand
    (fringe : char list)
    goal
    strategy
  = match fringe with
  | []                  -> None
  | n :: ns when goal n -> Some n
  | n :: ns             ->
    let fringe = strategy ns (expand n graph) in
    search graph expand fringe goal strategy

(* roadmap *)

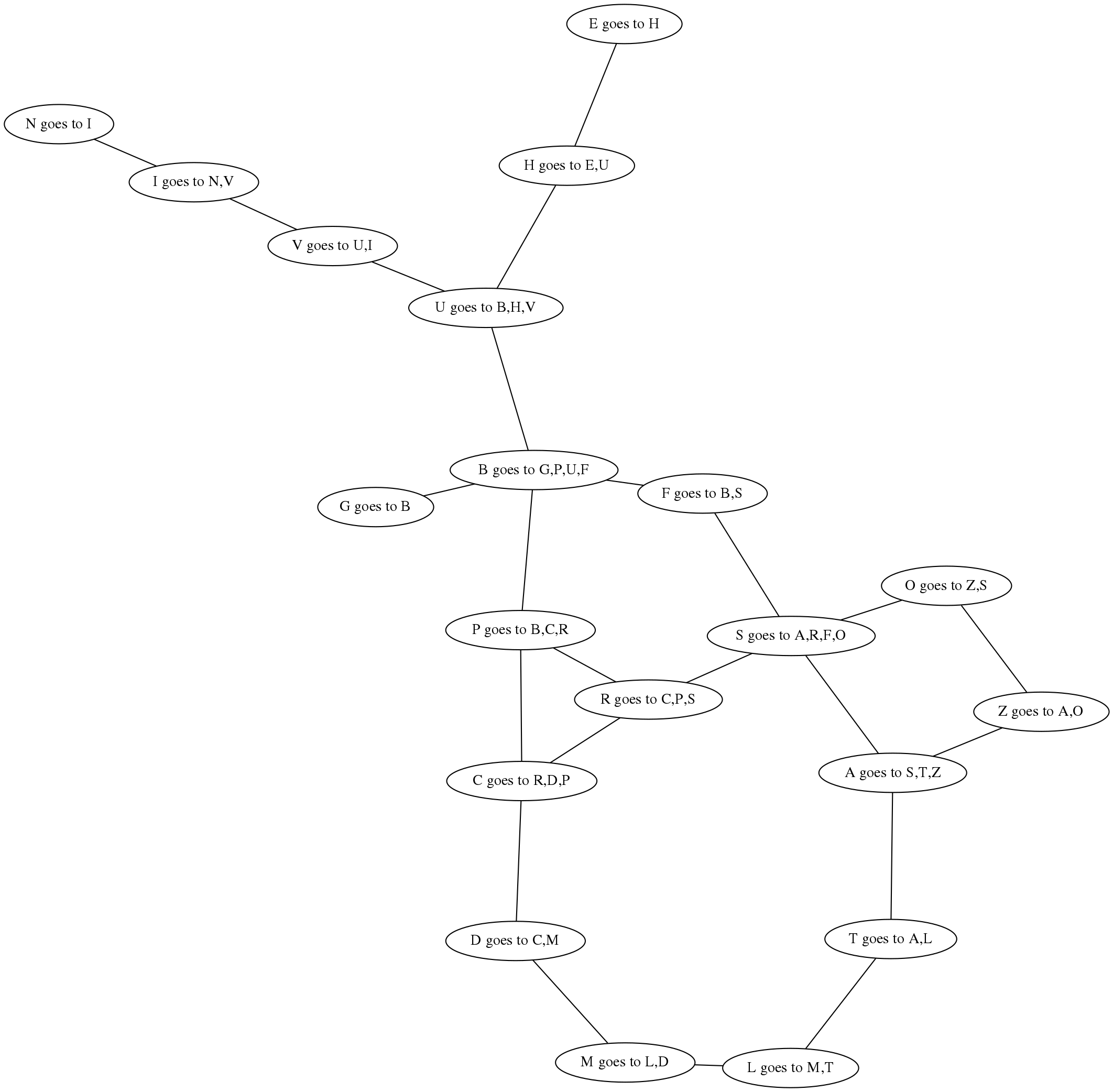
let roadmap =
  [ ('A', 'Z', 75);  ('A', 'S', 140); ('A', 'T', 118);
	('T', 'L', 111); ('L', 'M', 70);  ('M', 'D', 75);
	('D', 'C', 120); ('C', 'R', 146); ('R', 'S', 80);
	('R', 'P', 97);  ('S', 'O', 151); ('O', 'Z', 71);
	('S', 'F', 99);  ('F', 'B', 211); ('B', 'P', 101);
	('P', 'C', 138); ('B', 'G', 90);  ('B', 'U', 85);
	('U', 'H', 98);  ('H', 'E', 86);  ('U', 'V', 142);
	('V', 'I', 92);  ('I', 'N', 87)]

let rec expand node = function
  | [] -> []
  | (n1, n2, _) :: edges when n1 = node ->
    n2 :: expand node edges
  | (n1, n2, _) :: edges when n2 = node ->
    n1 :: expand node edges
  | _ :: edges -> expand node edges

(* Different type from 'goal' in the second version! *)

let goal n = (n = 'A')

(* Different type from 'strategy' in the second version! *)

let strategy xs ys = xs @ ys;;


(* In the lecture:

  let rec strategy = append;;

Equivalently, we could have written:

  let strategy xs ys = append xs ys;;

or:

  let strategy xs ys = xs @ ys;;


(* To use:

   search roadmap expand ['A'] goal strategy;;

 *)

Version 2

(* basic algo *)

let rec search
    (graph : (char * char * int) list)
    expand
    (fringe : char list)
    goal
    strategy
    visited
  = match fringe with
  | []                  -> None
  | n :: ns when goal n -> Some n
  | n :: ns             ->
    let fringe = strategy ns (expand n graph) (n :: visited) in
    search graph expand fringe goal strategy (n :: visited)

(* roadmap *)

let roadmap =
  [ ('A', 'Z', 75);  ('A', 'S', 140); ('A', 'T', 118);
	('T', 'L', 111); ('L', 'M', 70);  ('M', 'D', 75);
	('D', 'C', 120); ('C', 'R', 146); ('R', 'S', 80);
	('R', 'P', 97);  ('S', 'O', 151); ('O', 'Z', 71);
	('S', 'F', 99);  ('F', 'B', 211); ('B', 'P', 101);
	('P', 'C', 138); ('B', 'G', 90);  ('B', 'U', 85);
	('U', 'H', 98);  ('H', 'E', 86);  ('U', 'V', 142);
	('V', 'I', 92);  ('I', 'N', 87)]

let rec expand node = function
  | [] -> []
  | (n1, n2, _) :: edges when n1 = node ->
    n2 :: expand node edges
  | (n1, n2, _) :: edges when n2 = node ->
    n1 :: expand node edges
  | _ :: edges -> expand node edges

let goal n' n = (n = n')

let rec strategy fringe newnodes visited =
  let rec remove xs ys = match xs with
    | [] -> []
    | x :: xs ->
      if List.mem x ys
      then remove xs ys
      else x :: remove xs ys in 
  remove (newnodes @ fringe) visited


(* To use:

   search roadmap expand ['A'] (goal 'B') strategy [];;

 *)

Simplification of expand

As discussed in the tutorial.

let rec expand node edges = match edges with
  | [] -> []
  | (n1, n2, _) :: edges ->
          if n1 = node then n2 :: expand node edges
          else if n2 = node then n1 :: expand node edges
          else expand node edges

Things to explain

• Expand
• Strategy
• Goal

Visualisation of data from the graph